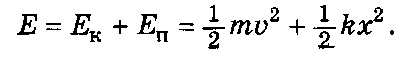|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
Вважатимемо, що потенціальна енергія маятника в найнижчому положенні кульки дорівнює нулю. Тому, коли маятник проходить положення рівноваги, його механічна енергія складається з однієї лише кінетичної енергії. З іншого боку, коли маятник перебуває в крайніх положеннях, кулька має лише потенціальну енергію. Внаслідок симетрії руху маятника в обидва боки від положення рівноваги потенціальна енергія кульки в обох крайніх положеннях однакова.
Сила натягу нитки не виконує роботи з переміщення кульки, оскільки її напрям завжди перпендикулярний до вектора швидкості кульки. Тому до кульки можна застосувати закон збереження енергії тіла. Згідно з цим законом сума кінетичної і потенціальної енергій кульки у всіх точках її траєкторії однакова і дорівнює значенням потенціальної енергії в крайніх положеннях і значенню кінетичної енергії в положенні рівно- ваги. Зрозуміло, що все це справедливо лише для коливань за відсутності затухання (тобто за відсутності сил тертя).
Повна механічна енергія під час коливань тіла на пружині чи математичного маятника дорівнює сумі кінетичної і потенціальної енергій
|
|
|
|
|
|
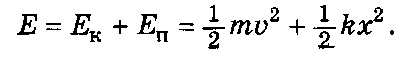
|
|
|
|
|
|
І кінетична, і потенціальна енергії періодично змінюються в часі, причому в ті моменти, коли кінетична енергія максимальна, потенціальна енергія перетворюється на нуль, і навпаки. Однак повна механічна енергія замкнутої коливальної системи, в якій відсутні сили опору, залишається згідно з законом збереження енергії незмінною. Вона дорівнює або потенціальній енергії в момент максимального відхилення від положення рівноваги, або ж кінетичній енергії в момент, коли тіло проходить положення рівноваги.
Таким чином, гармонічні коливання, які виникли в коливальній системі, стійкі і тривають як завгодно довго, якщо на коливальну систему не діють зовнішні сили (за рахунок роботи яких енергія системи могла б зростати) і в коливальній системі відсутні сили тертя та інші сили опору, які могли б призвести до розсіювання енергії системи.
|
|
|
|
|
|
|
|
|