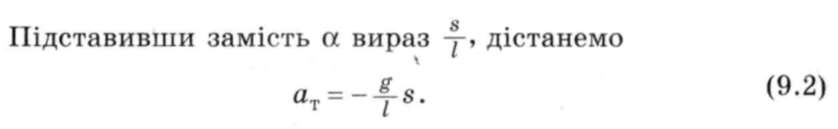|
|
|
|
|
|
|
|
|
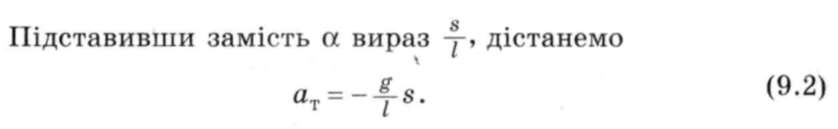
|
|
|
|
|
|
Це рівняння збігається з рівнянням руху кульки на пружині (9. 1)і Тут лише замість координати х стоїть довжина дуги s, а коефіцієнт пружності залежить не від жорсткості пружини і маси кульки, а від прискорення вільного падіння і довжини нитки. Однак знову прискорення (тепер тангенціальне) прямо пропорційне зміщенню (визначається дугою) кульки від положення рівноваги. Таким чином, ми дійшли важливого висновку, що рівняння руху кульки на пружині і маятника однакові. Зміщення кульки на пружині і маятника від положень рівноваги змінюються з часом за одним і тим самим законом, хоч сили, які зумовлюють коливання, мають різну фізичну природу.
|
|
|
|
|
|
§ 10 — ГАРМОНІЧНІ КОЛИВАННЯ
Знаючи, як пов'язані між собою прискорення і координата тіла, яке коливається, можна,за допомогою математичного аналізу знайти залежність координати від часу. Ми ж встановимо вид функції f(t), яка виражає залежність зміщення х від часу t, розглядаючи зв'язок між коливаннями маятника і рухом кульки по колу.
На малюнку 27 показано коливання кульки, яка ковзає вздовж осі ОХ, під дією сили пружності пружини F = -kx. Коливання кульки можна розглядати як проекцію колового руху кульки на вісь ОХ. Нехай А — рухомий радіус допоміжного кола, який відповідає найбільшому відхиленню кульки від положення рівноваги. Якщо обертати кульку по колу з такою кутовою швидкістю to, щоб проекція її руху збігалася з рухом кульки під дією сили пружності пружини, то її миттєве положення визначиться рівністю
|
|
|
|
|
|

|
|
|
|
|
|
|
|
|