|
нитки порівняно з масою кульки. Таким чином, замість реального фізичного маятника-кульки певного розміру на нитці, яка, звичайно, трохи деформується під час руху і має масу, можна розглядати просту модель: матеріальну точку, підвішену на нерозтяжній невагомій нитці. Така модель маятника називається математичним маятником. Підвішена на довгій тонкій нитці маленька кулька поводиться практично так само, як і математичний маятник.
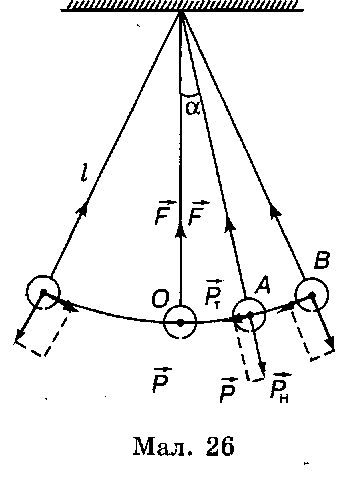
Виведемо маятник з положення рівноваги О до точки В (мал. 26) і відпустимо його — він коливатиметься. Розглянемо причину цих коливань.
Коли маятник перебуває в спокої у положенні А, сила тяжіння кульки Р і сила пружності нитки F діють на кульку під кутом одна до одної. Розкладемо силу тяжіння Р на дві складові: нормальну Рн, напрямлену вздовж нитки, і тангенціальну Рт, напрямлену перпендикулярно до нитки по дотичній до траєкторії кульки. Сила пружності нитки F і складова Рн сили тяжіння перпендикулярні до швидкості маятника і надають йому так званого нормального, або доцентрового, прискорення, напрямленого до центра дуги кола — траєкторії маятника. Робота цих сил дорівнює нулю, і тому згідно з теоремою про кінетичну енергію вони не змінюють модуля швидкості маятника. їх дія зумовлює лише безперервну зміну напряму швидкості, так що в будь-який момент часу швидкість напрямлена по дотичній до дуги кола.
Тангенціальна складова Рт сили тяжіння створює так зване тангенціальне прискорення, яке характеризує зміну модуля швидкості. Під дією складової Рт маятник починає рухатися по дузі кола вниз і швидкість його зростає. В міру руху маятника тангенціальна складова Рт сили тяжіння, напрямлена до положення рівноваги, зменшується і в момент, коли маятник проходить через положення рівноваги, вона перетворюється на нуль. Внаслідок інертності маятник рухатиметься далі, піднімаючись угору. При цьому складова Рт вже буде напрямлена проти швидкості. Тому швидкість маятника зменшується, і тим швидше, чим більший кут між ниткою і вертикаллю. Адже із збільшенням кута ця складо-
|
|
