|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мал. 27 Мал. 28
|
|
|
|
|
|
|
|
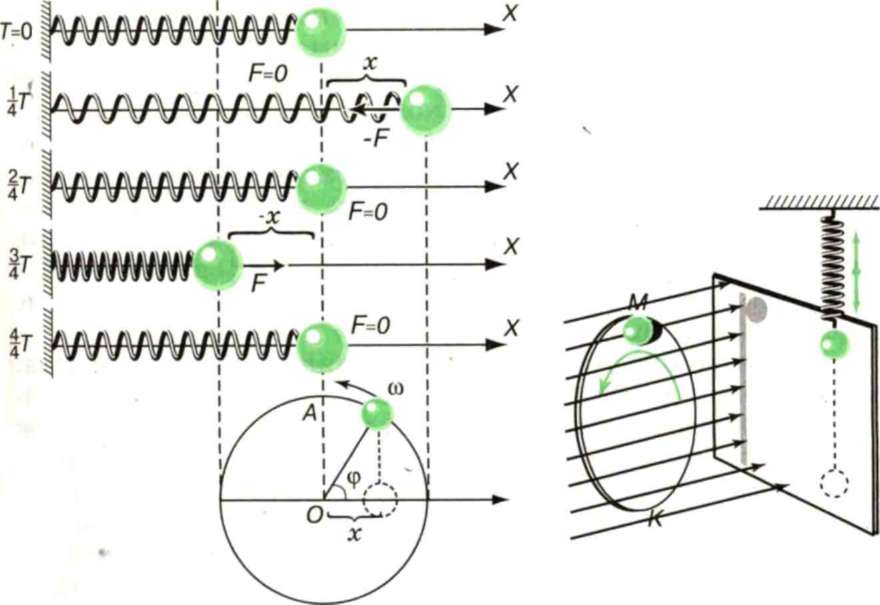
Аналогічно можна також порівняти коливання тіні кульки, закріпленої на диску, який обертається із сталою кутовою швидкістю со, і кульки пружинного маятника (мал. 28). Можна дібрати таку швидкість обертання диска, що рух тіні кульки на екрані повністю збігатиметься з рухом кульки пружинного маятника. Так само можна показати, що проекція рухомого радіуса диска ОМ на вертикальний діаметр змінюватиметься за законом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Проекції рухомого радіуса в обох описаних випадках можна розглядати як координати кульки, яка обертається по колу.
Таким чином, в зазначених випадках координата тіла, яке здійснює вільні коливання, змінюється з часом за законом синуса чи косинуса.
Періодичні зміни фізичної величини залежно від часу, які відбуваються за законом синуса або косинуса, називають гармонічними коливаннями.
Гармонічно можуть змінюватися різні фізичні величини: координата, швидкість, прискорення тощо. Спочатку розглядатимемо гармонічні коливання координати. Надалі ознайомимося з гармонічними змінами інших величин.
Важливою характеристикою коливального руху є амплітуда. Амплітудою гармонічних коливань називають модуль
|
|
|
|
|
|
|
|
|
|
|